User Area



elastic/inelastic shear buckling coefficient for plates

Log in to use the app

This app can be used for fast calculation of elastic/inelastic shear buckling coefficient for

plates subject to combined in-plane loads.

This coefficient is one of the most important structural design criteria in many engineering disciplines including Mechanics, Civil, Aerospace, Marine, etc. Typically, this parameter is evaluated through cumbersome FEM methods. This tool, which is developed based on the work of Dr. Alireza Jahanpour , can instead be used for easy and fast calculation of this coefficient. Users no longer have to limit themselves to certain FEM software packages such as Abaqus to calculate this parameter.


An analytical procedure may be quite complicated for the solution of the inelastic buckling equation of the plate with diverse boundary conditions and under multi-axial loadings. Thus, an explicit solution should be preferably developed using the theories of plasticity to predict the inelastic buckling load of plates.

—Jahanpour and Kouhia (2021)




About the Creator of the App



Dr. Alireza Jahanpour



Alireza is an Assistant Professor of Structural Engineering in Department of Civil Engineering at Malayer University, Iran. He is a well published researcher in the fields of Computational Mechanics, Structural Mechanics, Plates and Shells, Structural Stability and Analytical Solutions.

His research interests include:

  • Buckling and post-buckling behavior of thin-walled structures
  • Mechanics of composite materials
  • Seismic behavior of steel plate shear walls

Email: a.jahanpour@malayeru.ac.ir










Usage

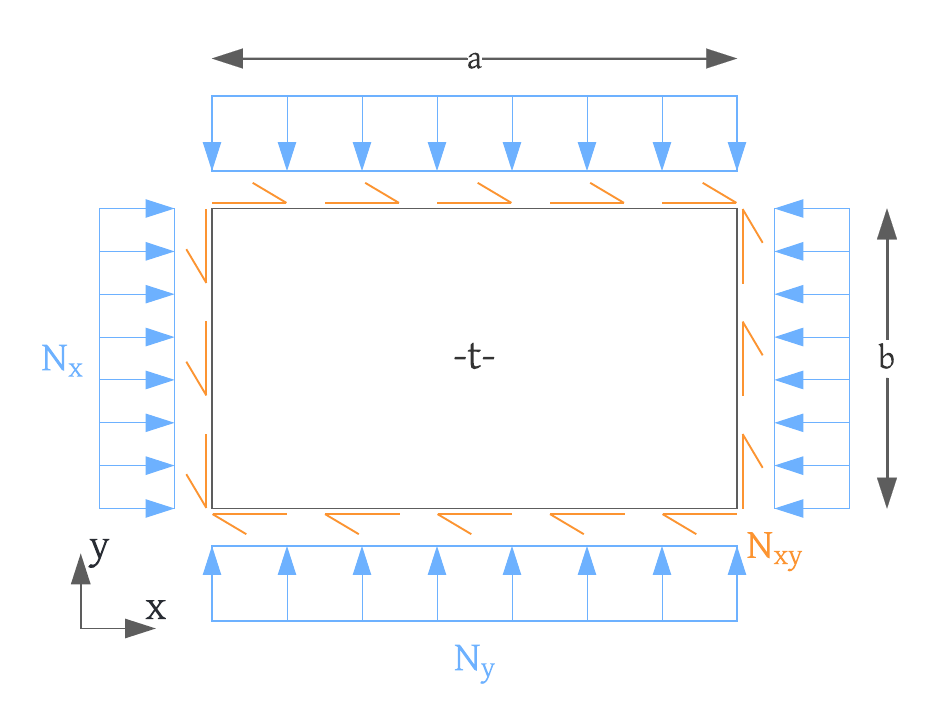
You only need to enter the below input parameters for your plate. Then the coefficient is calculated in a matter of seconds.


Input Parameters:


Parameter Description
boundary conditions Two types of boundary conditions are currently supported.
  • all edges simply supported, and
  • all edges fully clamped
aspect ratio $$ {\phi =\frac{a}{b}} $$

where

  • a = length of plate
  • b = width of plate
thickness ratio $$ {\lambda =\frac{b}{t}} $$

where

  • b = width of plate
  • t = thickness of plate
load ratio x $$ {\psi_x =\frac{N_x}{N_{xy}}} $$

where

  • $$ {N_x =t\sigma_x} $$
  • $$ {N_{xy} =t\tau} $$

$$ {N_x > 0: compression} $$

$$ {N_x < 0: tension} $$
load ratio y $$ {\psi_y =\frac{N_y}{N_{xy}}} $$

where

  • $$ {N_y =t\sigma_y} $$
  • $$ {N_{xy} =t\tau} $$

$$ {N_y > 0: compression} $$

$$ {N_y < 0: tension} $$
elastic Poisson's ratio $$ {\nu_e} $$
Ramberg-Osgood parameter 1 $$ {q} $$
Ramberg-Osgood parameter 2 $$ {\frac{E}{\sigma_{0.7E}}} $$
bucking mode $$ {n} $$
calculation of elastic/inelastic shear buckling coefficient of plates

Notes:

  • All of the above parameters are dimensionless.
  • Compression and tension loads are taken as positive and negative respectively.


to give it a try, register for a free account




For developers:

There also exists an API service for developers who are interested in using this functionality to build their own applications.

go to API documentation